فـترات التعـلُــــــم

المـؤشـــــــــــــرات

التقــــــــويـــــم

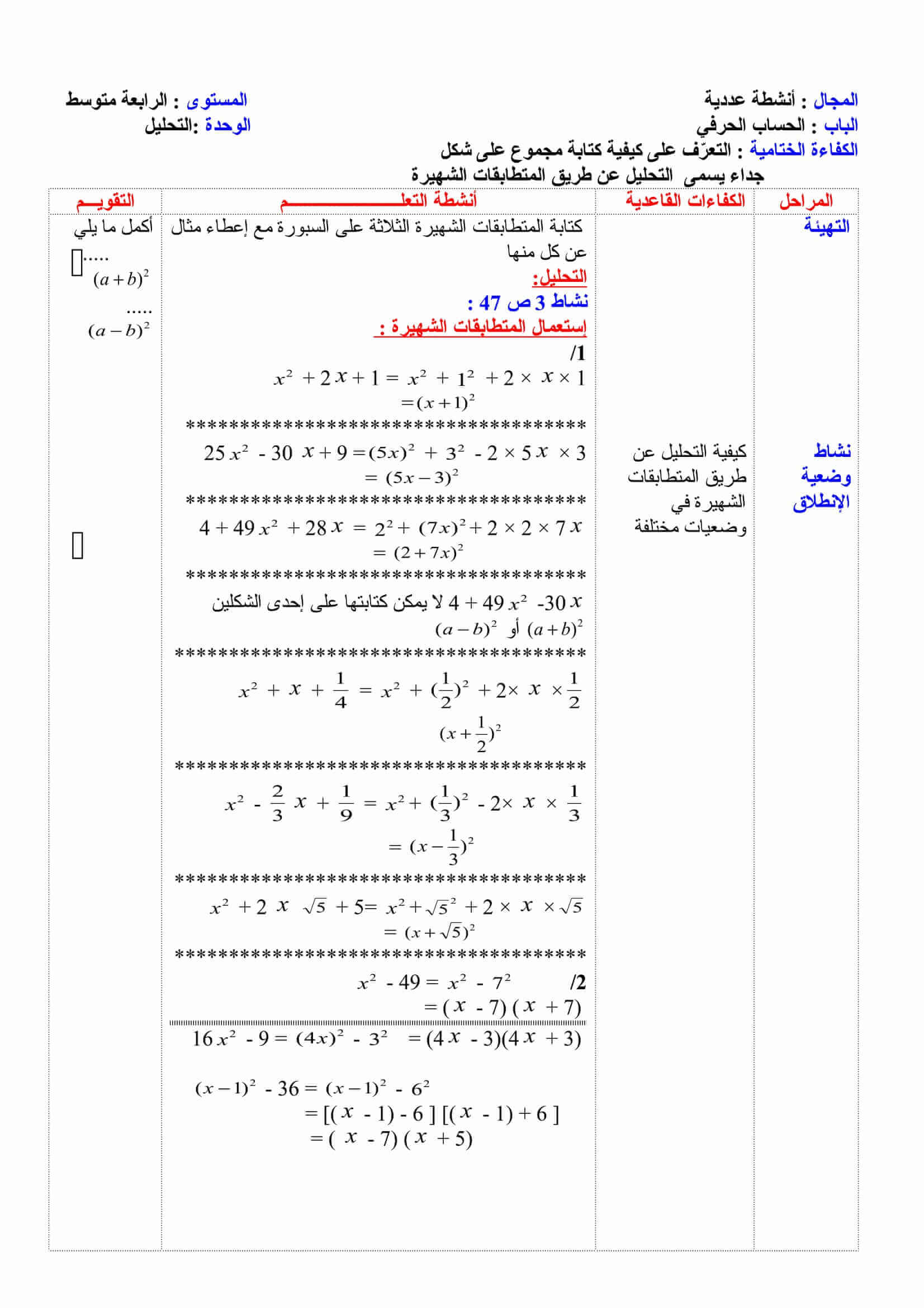
تـقـــديم النشـــــاط و إعطـــــــاء التَــعليـــمات

فتـــرة بنـــــاء التَـعلــــــــــُم

إعـادة الاستثمار

إعطاء أمثلة سريعة على السبورة عن كيفية حساب جيب تمام زاوية حادة في مثلث قائم و كيفية تطبيق نظرية طالس.

نشـــــــــــاط 01 ص 168:

(1) إتمام الفراغات.

(2) في الشكل: (AB) (OC) و (CD) (OC)

إذن: فإن (AB) // (CD) وحسب نظرية طالس فإن:

= = و بما أن: = فإن: AB ×OD = CD×OB

و بما أن = فإن: CD × OA =AB × OC

نعم المساويتان: = و = صحيحتان.

(وهذا بالاعتماد على المساويتان السابقتان)

ملاحظة : 5 × 4 = 10× 2 فإن: = و =

(3)

نلاحظ في جميع المثلثات أن: نسبة طول الضلع المقابل للزاوية 40° ثابتة.

طول الوتر

و أيضا: نسبة طول الضلع المقابل للزاوية 40° ثابتة.

طول الضلع المجاور للزاوية 40°

0.6 = sin 40° ؛ 0.8 = tan 40°

(4) في المثلث القائم ABC:

= ؛ =

= ؛ =

البحث: عـــــــــــــــــــــــــــــــــمـل فــــــــــــردي

الأخطاء المتوقَعة:

• أخطاء في تبيان النسب المتساوية واستنتاج المساويات.

الإجراءات الصحيحة:

• استنتاج المساويات وفهم جيب و ظل زاوية حادة.

العرض والمناقشة: عرض إجابات التلاميذ على السبورة ومناقشتها.

الحوصلة: كتابة المعرفة 01 و02 ص 173.

واجب منزلي رقم 1 و2 ص178.

– أذكر قانون حساب جيب تمام زاوية حادة في مثلث قائم؟

– ما هي الطريقة المتبعة لحساب كلا من جيب و ظل زاوية حادة في مثلث قائم؟

– لماذا جيب زاوية حادة يكون دائما محصور بين 0 و1؟

– هل ظل زاوية حادة يكون أحيانا أكبر من 1؟

مــراقبــــــة الأعمـــال

مقارنة الإجراءات المختلفة.

معـــالجــــة الأخطــاء

استنتاج المعرفة.