التمثيل المبياني لدالة عددية
التمثيل المبياني لدالة عددية
الدرس يتناول تعريف التمثيل المبياني لدالة عددية و يشرح كيفية إنشاء منحنى دالة عددية بإعتماد جدول للقيم و يتطرق لمفهوم الصورة و السابق و كيفية تحديدهما بإعتماد طريقة القراءة المبيانية
فهرس الدرس :
التمثيل المبياني لدالة عددية (تعريف)
التمثيل المبياني لدالة عددية والقراءة المبيانية.
أمثلة لمنحنيات دوال عددية.
التمثيل المبياني لدالة عددية (تعريف)
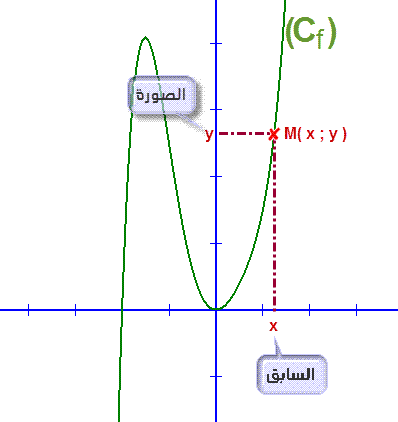
تعريف :
لتكن f دالة عددية وD مجموعة تعريفها و (O ; i ; j) معلما للمستوى.
التمثيل المبياني للدالة f مكون من جميع النقط (M(x ; y من المستوى بحيث (y = f(x و x ينتمي إلى D.
التمثيل المبياني للدالة f يسمى أيضا منحنى f و نرمز له ب (Cf) و (y = f(x تسمى معادلته.
ملاحظة
: نقول أن نقطة
(A(a ; b تنتمي إلى (Cf) يعني أن : a ينتمي إلى D و (b = f(a.
التمثيل المبياني لدالة عددية والقراءة المبيانية :
تمرين :
لتكن f الدالة المعرفة بمايلي :![]()
أحسب صورة 1 و حدد سوابق العدد 0.8
بإستعمال جدول للقيم أنشئ منحنى الدالة
حل مبيانيا المعادلة f(x) = 2
تأكد مبيانيا أن صورة 1 هي 3.2 و سابقي 0.8 هما 4 و 4-
الحل :
![]()
3.2 هي صورة 1 بالدالة f.
لكي نحدد سوابق العدد 0.8 بالدالة f يكفي ان نحل المعادلة f(x) = 0.8![]()
16/0,8 = x² + 4
x² + 4 = 20
x² = 20 – 4
x² = 16
x = 4 ,, x = -4
4 و 4- سوابق العدد 0.8 بالدالة f.
2- لكي ننشئ التمثيل المبياني للدالة سنستعين بجدول القيم حيث سنختار مجموعة من القيم ونحسب صورها بالدالة f :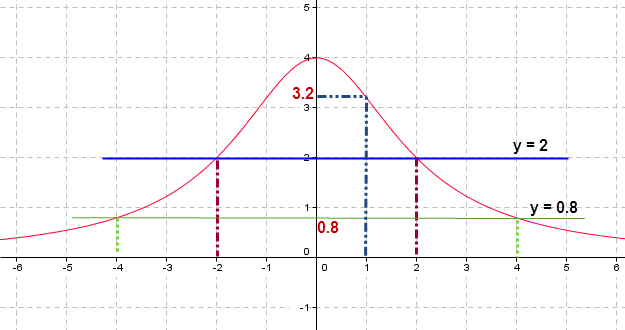
3- حل مبيانيا المعادلة f(x) = 2 يعني تحديد أفاصيل نقط تقاطع منحنى الدالة f ( بلون أحمر) و المستقيم ذو المعادلة y = 2 (بلون أزرق).
المستقيم ذو المعادلة y = 2 يقطع منحنى الدالة في نقطتين (A(-2 ; 2 و (B(2 ; 2.
إذن للمعادلة حلين هما 2 و 2-.
4- أنظر شكل
منهجية :
لتحديد صورة عدد حقيقي a مبيانيا بدالة عددية f يكفي أن نقرأ أرتوب النقطة التي أفصولها a على التمثيل المبياني للدالة f .
لتحديد سابق أو سوابق عدد حقيقي b مبيانيا بدالة عددية f يكفي أن نحدد أفصول أو أفاصيل نقط تقاطع التمثيل المبياني للدالة f و المستقيم و المعادلة y = b.
رجـــــــــــاء : رجاءا من كل الإخوة والأخوات الكرام الذين استفادو من هذه المعلومات وبقليل من الجهد ترك تعليق أو مشاركة الموضوع عبر احدى الأزرار الثلاثة twitter أو facebook أو +google ولكم جزيل الشكر





Comments are closed.