دراسة إشارة حدانية
دراسة إشارة حدانية
سندرس إشارة الحدانية ax + b و سنلخص هذه الدراسة في جدول يسمى جدول إشارة الحدانية ax + b ثم نستغل هذه الدراسة لحل بعض المتراجحات من الدرجة الأولى بمجهول واحد و متراجحات من الدرجة الثانية بمجهول واحد.
فهرس الدرس :
1 – دراسة إشارة الحدانية ax + b
2 – دراسة إشارة (ax + b)(cx +d)
3 – دراسة إشارة جداء يتضمن اكثر من حدانية
4 – دراسة خارج حدانيتين او أكثر.
5 – تدريبات سريعة لحل متراجحات بإستعمال جدول الإشارة
1 – دراسة أشارة الحدانية ax + b :
سننطلق من مثالين بسيطين، و لتكن مثلا الحدانية 2x + 3 و الحدانية 3x + 5- سندرس إشارتيهما من خلال التمرينين 1 و 2 ثم بعد ذالك نعمم بالنسبة ل ax + b
2x + 3 هي على شكل ax + b حيت : a = 2 و b = 3
3x + 5- هي على شكل ax + b حيت : a = -3 و b = 5
تمرين 1 :
1 – حل المعادلة : 2x + 3 = 0
2 – حل المتراجحة : 2x + 3 < 0 3 – حل المتراجحة : 2x + 3 > 0.
تمرين 2 :
1 – حل المعادلة : 3x + 5 = 0-
2 – حل المتراجحة : 3x + 5 < 0- 3 – حل المتراجحة : 3x + 5 > 0-
حل التمرين 1 :
1 . 2x + 3 = 0 يعني أن 2x = -3 أي أن : x = -3/2 إذن : {S = {-3/2
2 . 2x + 3 < 0 يعني أن 2x < -3 أي أن : x < -3/2 إذن : ] S = ] – ; -3/2 3 . 2x + 3 > 0 يعني أن 2x > -3 أي أن : x > -3/2 إذن : ] + ; S = ]-3/2
ما قمنا به في حل التمرين 1 يسمى دراسة إشارة الحدانية 2x + 3 و هذا يعني أنه :
إذاكان x < -3/2 فإن 2x + 3 < 0 إذاكان x = -3/2 فإن 2x + 3 = 0 إذاكان x >-3/2 فإن 2x + 3 > 0
و يمكن أن نلخص هذه الدراسة في الجدول التالي :
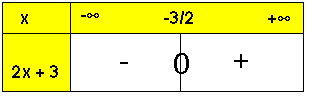
حل التمرين 2 :
1 . 3x + 5 = 0- يعني أن 3x = -5- أي أن : x = 5/3 إذن : {S = {5/3
2 . 3x + 5 < 0- يعني أن 3x < -5- أي أن : x > 5/3 إذن : ] + ; S = ]5/3
3 . 3x + 5 > 0- يعني أن 3x > -5- أي أن : x < 5/3 إذن : ] S = ] – ; 5/3
ما قمنا به في حل التمرين 2 يسمى دراسة إشارة الحدانية 3x + 5- و هذا يعني أنه :
إذاكان x < 5/3 فإن 3x + 5 > 0-
إذاكان x = 5/3 فإن 3x + 5 = 0-
إذاكان x >5/3 فإن 3x + 5 < 0-
و يمكن أن نلخص هذه الدراسة في الجدول التالي :
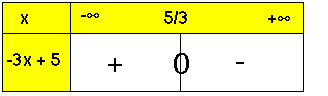
بصفة عامة :
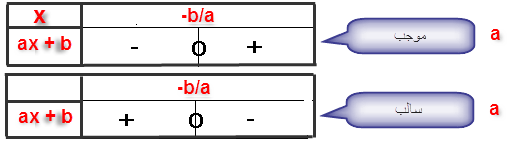
نعتبر الحدانية ax + b حيث a يخالف 0
إذا كان x ≥ -b/a فإن ax + b و a لهما نفس الإشارة
إذا كان x ≤ -b/a فإن ax + b و a- لهما نفس الإشارة
تمرين تطبيقي : أدرس إشارة كل من الحدانيات التالية :
A = 3x + 1;; B = -2x -2 ;; C = 4x + 2 ;; D = -3x + 2
E = 1 – 2x ;; F = (2/3)x + 1;; G = -2 + 4x ;; H = (5/4) – 2x
دراسة إشارة (ax + b)(cx +d) :
قاعدة :
لدراسة إشارة جداء يكفي أن ندرس إشارة كل من عامليه.
ليكن P جداء لعاملين : P = a.b
إذا كان ل a و b نفس الإشارة فإن الجداء P موجب.
إذا كان ل a و b إشارتين مختلفتين فإن الجداء P سالب.
مثال : حدد إشارة (P(x) = (4x – 1)(2 – 3x
نحدد إشارة 4x – 1
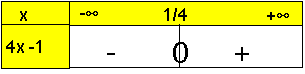
جدول إشارة 4x – 1
نحدد إشارة ×3 – 2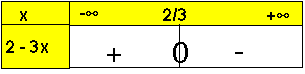
جدول إشارة ×3 – 2
نلخص الجدولين السابقين في جدول إشارة (P(x) = (4x – 1)(2 – 3x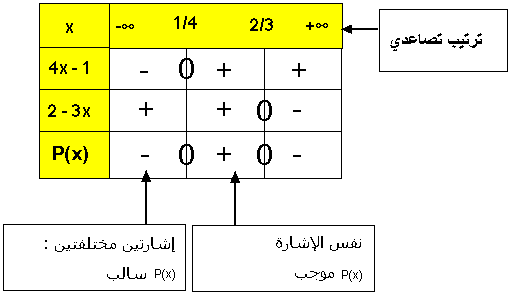
خلاصة :
(P(x موجبة قطعا إذاكان x ينتمي إلى المجال : ]1/4 ; 2/3[
(P(x سالبة قطعا إذاكان x ينتمي إلى المجال :
]- ; 1/4[ U ]2/3 ;+ [
(P(x منعدمة او تساوي 0 إذاكان : x = 1/4 أو x = 2/3
تمرين تطبيقي : حدد إشارة ما يلي
A = (2x + 1)(-2x +2)
B = (-5x + 2)(-3x + 2)
C = (1 – 2x)(x + 1)
D = (-2x + 4)(4 – 3x)
دراسة إشارة جداء يتضمن أكثر من حدانيتين :
نعتمد دائما نفس المبدأ حتى في دراسة جداء يتضمن أكثر من حدانيتين
مثال : حدد إشارة (3x(-2x – 1)( 2 – 3x:
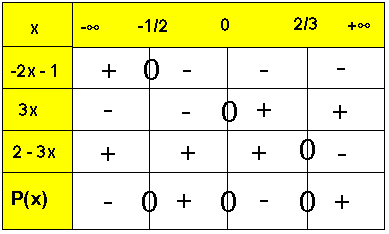
خلاصة :
(P(x موجبة قطعا إذاكان ينتمي إلى المجال :
]- 1/2 ; 0[ U ]2/3 ; +[
(P(x سالبة قطعا إذاكان ينتمي إلى المجال :
]- ; – 1/2[ U ]0 ; 2/3[
(P(x منعدمة او تساوي 0 إذاكان : x = 1/4 أو x = 2/3
تمرين تطبيقي : حدد إشارة مايلي
A = (3x + 1)(4x + 2)(-3x + 2)
B = (1 – 2x)(x + 1)(-2 + 4x)
4 – دراسة إشارة الخارج :
لكي تحدد إشارة خارج حدانيتين :
تتأكد اولا ان البسط و المقام على شكل حدانية أو جداء حدانيات
تنشئ جدول الإشارة لكل عوامل هذا الخارج :
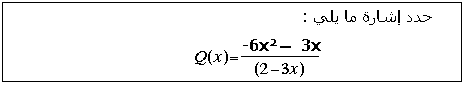
أولا: نعمل البسط ونكتب 6x² – 3x- على شكل جداء حدوديتين :
-6x² + 3x = 3x( -2x – 1 )
أي أن :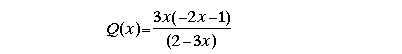
جدول إشارة (Q(x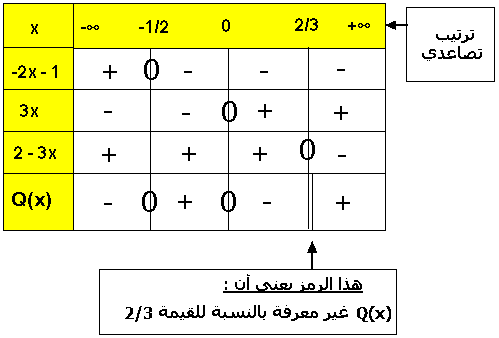
تمرين تطبيقي : حدد إشارة ما يلي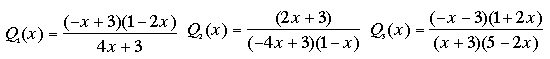
منهجية و طريقة :
حل المتراجحة 3x + 2)x > 0) مثلا يعني إيجاد جميع قيم المجهول x التي من أجلها يكون التعبير الجبري 3x + 2)x) موجب قطعا.
إذن يكفي إنشاء جدول إشارة الجداء 3x + 2)x) ومن تم نحدد قيم المجهول التي تحقق 3x + 2)x > 0).
مجموعة حلول هذه المتراجحة هي :
S = ]- ; -2/3[ U ]0 ; +[
تمرين تطبيقي :
حل في مجموعة الأعداد الحقيقية المتراجحات التالية :
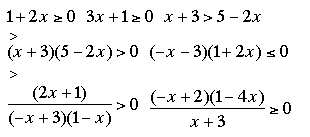
رجـــــــــــاء : رجاءا من كل الإخوة والأخوات الكرام الذين استفادو من هذه المعلومات وبقليل من الجهد ترك تعليق أو مشاركة الموضوع عبر احدى الأزرار الثلاثة twitter أو facebook أو +google ولكم جزيل الشكر




Comments are closed.